Schweizer Sturmforum

@Balz: stimmt nicht, denn der Körper in 100 m Höhe bewegt sich ja etwas schneller als die Oberfläche, um sich in 24 Stunden um die Erde zu drehen. Er hat ja in der gleichen Zeit (24 Stunden) mehr Weg zurückzulegen (genau 100*2*Pi Meter).

Wenn er dann fällt, bewegt er sich ja während des Fall immer noch schneller in Ostrichtung als die Oberfläche, d.h. während des Falls bewegt er sich gegenüber der Oberfläche nach Osten.

Ch.

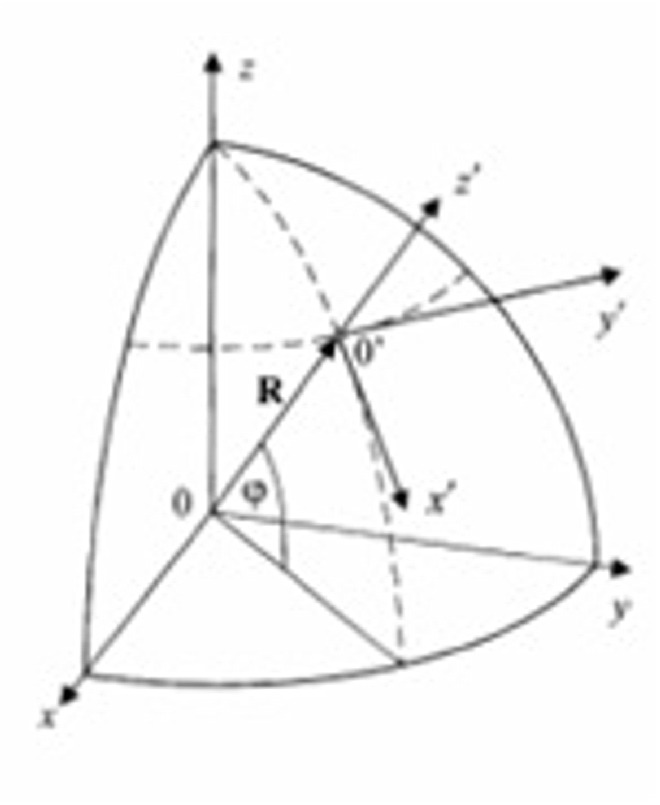
Apropos: das ist das gleiche wie die Corioliskraft, denn nimm mal die Erde am Äquator durchgeschnitten: dann hast Du das Problem auf 2 Dimensionen reduziert, die Äquatorebene ist dann unser Experimentierfeld. Dann kannst Du Dir die Corioliskraft wieder vorstellen, oder? Oder anders gesagt ist das der Pirouetten-Effekt.

Hoi Fabienne

Es ist eigentlich ganz einfach:

Die einzige Formel, die man dazu wissen muss, ist diejenige über den Umfang eines Kreises:

u = 2*r*Pi

wobei
u = Umfang
r = Kreisradius

Wir nehmen an die Erde sei eine perfekte Kugel und der Äquator ein perfekter Kreis. Nun verlängern wir die Schnur um zehn Meter, verlängern den Umfang also um zehn Meter. Somit muss sich auch der Radius verlängern. Aber um wieviel? Diese Unbekannte nennen wir y. Somit haben wir eine neue Gleichung, basierend auf der Gleichung über den Umfang eines Kreises:

u+10 = 2*(r+y)*Pi

u ist der ursprüngliche Umfang und der ist ja bekanntlich 2*r*Pi, also haben wir:

(2*r*Pi) + 10 = 2*(r+y)*Pi

Dann teilen wir durch 2*Pi und erhalten:

r + (5/Pi) = r+y

oder y = 5/Pi

Wir sehen: die Variable r fällt weg!

Allgemein gerechnet ergibt y:

y = x/(2*Pi)

wobei x die Verlängerung der Schnur ist.

Gruss Chrigi


- Editiert von Christian Matthys am 15.11.2005, 13:00 -

Hoi Chrigi

Vielen Dank für deine Mühe, aber du hast meinen Einwurf missverstanden, dessen Aussage ist: Mathematisch wirst du mir das niemals erklären können. Ich werde mal versuchen, das mit zwei verschieden grossen runden Gegenständen und einer Schnur in meinem Haushalt nachzuvollziehen. Wenn der Abstand von einer um 10 cm verlängerten Schnur um eine Tasse und um einen grossen Topf gleich gross ist, bin ich überzeugt, vorher nicht.

Ja ja, wundert euch nur...

Hoi Fabienne

Achso hast du das gemeint. Ich kanns eigentlich auch kaum glauben und war mir sogar etwas unsicher, ob ich wirklich alles richtig gerechnet habe.

Vielleicht kann man's so besser verstehen/begreifen: Der Umfang eines Kreises ist aufgrund der Formel u = 2*r*Pi direkt proportional zum Radius (da 2*Pi eine feste Zahl ist). Somit ist auch jedes Teilstück des Radius direkt proportional zu einem Teilstück des Umfangs. Die Proporionalität ergibt sich aus der festen Zahl 2*Pi, ist also nicht abhängig von der Grösse des Kreises. Somit müsste ein Radius-Teilstück von 10 Metern immer einem Umfang-Teilstück von 10*2*Pi (also ungefähr 62.8 Metern) entsprechen.

Nehmen wir nun an die Kugel (oder der Kreis) sei verschwindend klein und der Umfang ebenfalls, dann ist die Vergrösserung des Radius y gemäss der Formel

y = x/(2*Pi)

wobei x = Verlängerung des Umfangs (für unser Beispiel z.B. gerundet 62.8m)

ungefähr 10 Meter (wird x exakt gerechnet in Abhängigkeit von Pi, dann ist y natürlich auch genau 10 Meter). Da der Anfangskreis verschwindend klein war, können wir die Verlängerung des Radius gleich als echten Radius eines neuen Kreises betrachten. Gemäss der Formel u = 2*r*Pi müsste dann also 62.8 [m] = 2*10[m]*Pi sein…. was natürlich stimmt. q.e.d.

Gruss Chrigi
- Editiert von Christian Matthys am 15.11.2005, 15:00 -

Hoi zämme,

die Ostabweichung beträgt 2.19834 cm.

auf die Details komme ich noch...

Grüsse

@cyba: hoffentlich kannst Du mir auch erklären, wo ich falsch gedacht habe... :O

Ch.

Hoi zämme, hier nun ein paar Details.

Ausgegangen bin ich von der folgenden Situation:

Koordinatensysteme



Dabei ist S(x,y,z) das Inertialsystem , also das Ruhesystem, in welchem das Trägheitsprinzip gilt. Wie schon erwähnt, wird der Umlauf um die Sonne etc. vernachlässigt. Das System S'(x',y',z') ist ein beschleunigtes Bezugssystem , der Geschwindigkeitsvektor ändert zwar nicht seinen Betrag, dafür aber seine Richtung (kontinuierlich), also muss eine Kraftwirkung, sprich Beschleunigung, vorliegen.

Annahmen

Ich treffe die folgenden Annahmen:

1.Die Winkelgeschwindigkeit der Erde soll als klein angenommen werden
2.Der Fall erfolgt reibungsfrei
3.g ist für "kleinere" Höhen konstant
4.Bewegung der Erde um die Sonne, Polschwankungen, etc. werden vernachlässigt

Bewegungsgleichung im beschleunigten Bezugssystem

Die Herleitung ist ziemlich aufwändig (bei Interesse-einfach fragen). Das Resultat ist



Der erste Term auf der rechten Seite ist die Kraft, welche durch die Umgebung verursacht wird (beim freien Fall die Gewichtskraft mg). Der zweite Term ist die Corioliskraft . Der dritte die Kreisel-, der vierte die Zentrifugal- und der letzte die Massenträgheits- oder Führungskraft. Die vier letzten Kräfte auf der rechten Seite werden auch Scheinkräfte genannt, sie "existieren" ausschliesslich in einem beschleunigten Bezugssystem. Die Komponentenschreibweise der obigen Gleichung ist dann



Ein paar Vereinfachungen: Die Kreiselkraft verschwindet, da die Winkelgeschwindigkeit konstant ist, die "Omega-Quadrat"-Terme können vernachlässigt werden, weil Omega klein ist, und die Führungskraft ist in unserem Fall nicht vorhanden.

Die Winkelgeschwindigkeit der Erde kann man dann noch mit Koordinaten des Systems S' ausdrücken (Trigo) und die wirkende Kraft F ist dann die Gewichtskraft (wobei g nur eine z-Komponente hat). Die Bewegungsgleichungen in den drei Komponenten lauten dann:





Jetzt kann man ein wenig mit den Anfangsbedingungen spielen, ein wenig integrieren, ein wenig einsetzen, und man erhält für die Ostablenkung in Abhängigkeit der Fallhöhe:



Das heisst

Aus dieser Gleichung sieht man sofort, dass die Ostablenkung am Äquator maximal wird. Man sieht auch, dass wir an den Polen keine Ostablenkung haben.

Ich habe folgendes Ergebnis erhalten:



also 2.19834 cm am Äquator.

Grüsse

@Christian-möglicherweise ist Deine Vektoraddition für die Horizontalgeschwindigkeit falsch...Frage der Machbarkeit...

Ah dann hatte ich wohl doch recht. Aber es war mir zugegebenermassen etwas zu mühsam, die ganzen Vektoren hier reinzuschreiben.

Gruss Michael

Das ist noch eine interessante Frage:

Warum können in der unmittelbaren Nähe des Äquators keine Wirbel erzeugt werden?

Am Äquator ist der Geschwindigkeitsvektor der Luft und der Vektor der Winkelgeschwindigkeit linear abhängig, d.h. der eine ist ein Vielfaches des anderen. Die beiden Vektoren spannen keine Ebene mehr auf, der Flächeninhalt des "aufgespannten Parallelogrammes" beim Vektorprodukt ist deshalb null, somit auch die Corioliskraft.

(a x b = 0 a,b linear abhängig)

@Michael: weißt Du denn, was an der "trivialen" Idee von mir falsch ist?

Ch.